Test Review Perform the Indicated Operation Write Your Answer in 1 +bi Form Worksheet

Learning Outcomes

• Add or Subtract fractions.
• Simplify fractions.
• Multiply fractions.
• Divide fractions.

Math students and working adults often discover their noesis of how to add together, subtract, multiply, and separate fractions has grown rusty with disuse.  We tend to rely on calculators to do a lot of the work of fractions for united states. College Algebra, though, builds up some important techniques for handling expressions and equations that are based on operations on fractions. So information technology is of import to refamiliarize yourself with these skills. This section volition remind you lot how to practice operations on fractions. As you work through the rest of the course, you can return this department as needed for a quick reminder of operations on fractions.

Before we get started, allow's define some terminology.

• production:the consequence of  multiplication
• gene: something existence multiplied – for  [latex]3 \cdot 2 = vi[/latex] , both [latex]three[/latex] and [latex]2[/latex] are factors of [latex]half dozen[/latex]
• numerator: the meridian part of a fraction – the numerator in the fraction [latex]\Large\frac{2}{3}[/latex] is [latex]ii[/latex]
• denominator: the bottom function of a fraction – the denominator in the fraction [latex]\Large\frac{2}{3}[/latex] is [latex]iii[/latex]

A Annotation About Instructions

Sure words are used in math textbooks and past teachers to provide students with instructions on what to do with a given problem. For instance, you may see instructions such as find or simplify. It is important to understand what these words hateful then you can successfully piece of work through the problems in this course. Hither is a short list of some problem instructions along with their descriptions every bit they will exist used in this module.

Instruction	Interpretation
Find	Perform the indicated mathematical operations which may include addition, subtraction, multiplication, division (after, use of the wordfind will exist expanded to solving equations, as infind the value of variable).
Simplify	1) Perform the indicated mathematical operations including add-on, subtraction, multiplication, division 2) Write a mathematical statement in smallest terms and then there are no other mathematical operations that tin can be performed—often constitute in problems related to fractions and the order of operations
Evaluate	1) Perform the indicated mathematical operations including addition, subtraction, multiplication, partitioning 2) Substitute a given value for a variable in an expression and then perform the indicated mathematical operations
Reduce	Write a mathematical statement in smallest or everyman terms so there are no other mathematical operations that can exist performed—oftentimes establish in problems related to fractions or division

Add Fractions

When you need to add or subtract fractions, you will need to get-go make sure that the fractions have the same denominator. The denominator tells you how many pieces the whole has been broken into, and the numerator tells you how many of those pieces yous are using.

The "parts of a whole" concept tin be modeled with pizzas and pizza slices. For example, imagine a pizza is cut into [latex]4[/latex] pieces, and someone takes [latex]1[/latex] piece. At present, [latex]\Large\frac{one}{4}[/latex] of the pizza is gone and [latex]\Large\frac{3}{four}[/latex] remains. Note that both of these fractions have a denominator of [latex]four[/latex], which refers to the number of slices the whole pizza has been cut into. What if you lot take another pizza that had been cut into [latex]viii[/latex] equal parts and [latex]iii[/latex] of those parts were gone, leaving [latex]\Large\frac{5}{viii}[/latex]?

How tin can you describe the total amount of pizza that is left with 1 number rather than two different fractions? You need a mutual denominator, technically chosen the least common multiple. Remember that if a number is a multiple of another, you tin can split up them and take no remainder.

Ane fashion to find the least mutual multiple of 2 or more numbers is to outset multiply each by [latex]1, ii, 3, four[/latex], etc.  For instance, find the to the lowest degree mutual multiple of [latex]ii[/latex] and [latex]5[/latex].

First, listing all the multiples of [latex]two[/latex]:	Then list all the multiples of 5:
[latex]2\cdot i = 2[/latex]	[latex]five\cdot 1 = 5[/latex]
[latex]two\cdot 2 = 4[/latex]	[latex]5\cdot two = 10[/latex]
[latex]2\cdot 3 = 6[/latex]	[latex]v\cdot iii = 15[/latex]
[latex]two\cdot 4 = eight[/latex]	[latex]five\cdot iv = 20[/latex]
[latex]ii\cdot v = 10[/latex]	[latex]five\cdot 5 = 25[/latex]

The smallest multiple they accept in common will be the mutual denominator to use to rewrite each fraction into equivalent fractions. See the instance below for a demonstration of our pizza trouble.

Example

Ane pizza, cutting into four slices, has 1 missing. Another pizza of the same size has been cutting into 8 pieces, of which three have been removed. Depict the total amount of pizza left in the two pizzas using common terms.

To add together fractions with unlike denominators, first rewrite them with like denominators. So add together or subtract the numerators over the common denominator.

Adding Fractions with Dissimilar Denominators

1. Find a mutual denominator.
2. Rewrite each fraction as an equivalent fraction using the common denominator.
3. At present that the fractions have a common denominator, you can add the numerators.
4. Simplify by canceling out all common factors in the numerator and denominator.

Simplify a Fraction

It is a common convention in mathematics to present fractions in lowest terms. Nosotros phone call this dosimplifying or reducing the fraction, and it tin can be accomplished past canceling (dividing) the common factors in a fraction's numerator and denominator.  We can exercise this because a fraction represents division, and for any number [latex]a[/latex], [latex]\dfrac{a}{a}=one[/latex].

For example, to simplify [latex]\dfrac{half-dozen}{9}[/latex] you tin rewrite [latex]6[/latex]and [latex]nine[/latex] using the smallest factors possible as follows:

[latex]\dfrac{vi}{9}=\dfrac{ii\cdot3}{3\cdot3}[/latex]

Since there is a [latex]3[/latex] in both the numerator and denominator, and fractions tin be considered division, we can split the [latex]3[/latex] in the top past the [latex]3[/latex] in the bottom to reduce to [latex]1[/latex].

[latex]\dfrac{six}{9}=\dfrac{two\cdot\cancel{iii}}{iii\cdot\cancel{3}}=\dfrac{2\cdot1}{3}=\dfrac{2}{three}[/latex]

In the next case y'all are shown how to add two fractions with different denominators, then simplify the answer.

Example

Add together [latex]\Large\frac{2}{3}+\Large\frac{1}{5}[/latex]. Simplify the answer.

You tin find a common denominator by finding the common multiples of the denominators. The least common multiple is the easiest to employ.

Instance

Add [latex]\Big\frac{iii}{7}+\Large\frac{2}{21}[/latex]. Simplify the reply.

In the following video you will see an example of how to add together two fractions with unlike denominators.

Y'all can also add more than two fractions as long every bit you lot first find a common denominator for all of them. An case of a sum of three fractions is shown below. In this instance, you will employ the prime number factorization method to find the LCM.

Think Near Information technology

Add [latex]\Large\frac{3}{iv}+\Large\frac{i}{six}+\Large\frac{5}{8}[/latex].  Simplify the answer and write every bit a mixed number.

What makes this instance unlike than the previous ones? Use the box beneath to write downward a few thoughts about how you lot would add together iii fractions with different denominators together.

Subtract Fractions

Subtracting fractions follows the same technique equally adding them. First, decide whether or not the denominators are alike. If not, rewrite each fraction equally an equivalent fraction, all having the same denominator.  Below are some examples of subtracting fractions whose denominators are not alike.

Case

Subtract [latex]\Large\frac{1}{5}-\Large\frac{1}{six}[/latex]. Simplify the answer.

The case below shows how to use multiples to find the least common multiple, which volition be the least common denominator.

Case

Subtract [latex]\Large\frac{5}{6}-\Large\frac{1}{iv}[/latex]. Simplify the answer.

In the following video yous will come across an example of how to subtract fractions with unlike denominators.

Multiply Fractions

Only as you add together, subtract, multiply, and divide when working with whole numbers, y'all also apply these operations when working with fractions.   There are many times when information technology is necessary to multiply fractions. A model may assist you lot sympathize multiplication of fractions.

When you multiply a fraction by a fraction, you are finding a "fraction of a fraction." Suppose you accept [latex]\Large\frac{3}{iv}[/latex] of a candy bar and you want to find [latex]\Large\frac{1}{ii}[/latex] of the [latex]\Large\frac{3}{4}[/latex]:

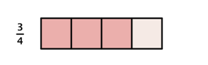
Past dividing each fourth in half, you can divide the processed bar into eighths.

Then, choose half of those to get [latex]\Big\frac{3}{viii}[/latex].

In both of the above cases, to observe the respond, you tin can multiply the numerators together and the denominators together.

Multiplying Two Fractions

[latex]\Big\frac{a}{b}\cdot\Large\frac{c}{d}=\Big\frac{a\cdot c}{b\cdot d}=\Big\frac{\text{product of the numerators}}{\text{product of the denominators}}[/latex]

Multiplying More than 2 Fractions

[latex]\Large\frac{a}{b}\cdot\Large\frac{c}{d}\cdot\Large\frac{due east}{f}=\Big\frac{a\cdot c\cdot eastward}{b\cdot d\cdot f}[/latex]

Case

Multiply [latex]\Large\frac{2}{3}\cdot\Big\frac{4}{5}[/latex]

To review: if a fraction has common factors in the numerator and denominator, nosotros can reduce the fraction to its simplified form by removing the mutual factors.

For instance,

• Given [latex]\Large\frac{8}{xv}[/latex], the factors of [latex]8[/latex] are: [latex]ane, 2, iv, 8[/latex] and the factors of [latex]15[/latex] are: [latex]one, 3, 5, 15[/latex].  [latex]\Big\frac{viii}{xv}[/latex] is simplified considering in that location are no common factors of [latex]8[/latex] and [latex]xv[/latex].
• Given [latex]\Large\frac{10}{xv}[/latex], the factors of [latex]ten[/latex] are: [latex]1, two, five, 10[/latex] and the factors of [latex]15[/latex] are: [latex]1, 3, five, 15[/latex]. [latex]\Large\frac{10}{15}[/latex] is non simplified because [latex]five[/latex] is a common factor of [latex]x[/latex] and [latex]15[/latex].

Y'all can simplify starting time, earlier you multiply two fractions, to brand your work easier. This allows you to piece of work with smaller numbers when you multiply.

In the following video you will see an example of how to multiply two fractions, and so simplify the respond.

Call up About Information technology

Multiply [latex]\Large\frac{2}{3}\cdot\Large\frac{1}{4}\cdot\Big\frac{3}{5}[/latex]. Simplify the answer.

What makes this example different than the previous ones? Use the box below to write down a few thoughts nearly how yous would multiply three fractions together.

Split up Fractions

There are times when you need to employ division to solve a trouble. For instance, if painting one coat of paint on the walls of a room requires [latex]three[/latex] quarts of paint and yous have a saucepan that contains [latex]six[/latex] quarts of paint, how many coats of paint tin you pigment on the walls? You divide [latex]6[/latex] by [latex]3[/latex] for an answer of [latex]2[/latex] coats. There will also be times when you need to divide past a fraction. Suppose painting a cupboard with one coat only required [latex]\Large\frac{i}{2}[/latex] quart of paint. How many coats could be painted with the half dozen quarts of paint? To observe the answer, you need to divide [latex]2[/latex] by the fraction, [latex]\Large\frac{one}{2}[/latex].

Before nosotros begin dividing fractions, let'southward comprehend some important terminology.

• reciprocal: two fractions are reciprocals if their product is [latex]1[/latex] (Don't worry; nosotros volition show you examples of what this means.)
• quotient: the result of division

Dividing fractions requires using the reciprocal of a number or fraction. If you multiply 2 numbers together and get [latex]one[/latex] every bit a result, and so the two numbers are reciprocals. Here are some examples of reciprocals:

Original number	Reciprocal	Production
[latex]\Large\frac{3}{4}[/latex]	[latex]\Large\frac{4}{3}[/latex]	[latex]\Big\frac{3}{iv}\cdot\Large\frac{4}{3}=\Big\frac{3\cdot 4}{4\cdot 3}=\Large\frac{12}{12}=1[/latex]
[latex]\Big\frac{i}{2}[/latex]	[latex]\Large\frac{2}{1}[/latex]	[latex]\Large\frac{1}{2}\cdot\Large\frac{2}{1}=\Large\frac{ane\cdot2}{2\cdot1}=\Large\frac{2}{2}=one[/latex]
[latex] iii=\Large\frac{3}{1}[/latex]	[latex]\Big\frac{1}{3}[/latex]	[latex]\Large\frac{3}{i}\cdot\Big\frac{1}{iii}=\Big\frac{3\cdot ane}{1\cdot 3}=\Large\frac{3}{3}=one[/latex]
[latex]two\Big\frac{1}{3}=\Large\frac{7}{3}[/latex]	[latex]\Large\frac{iii}{7}[/latex]	[latex]\Large\frac{7}{three}\cdot\Large\frac{three}{vii}=\Large\frac{seven\cdot3}{three\cdot7}=\Large\frac{21}{21}=\normalsize one[/latex]

Sometimes nosotros call the reciprocal the "flip" of the other number: flip [latex]\Large\frac{ii}{5}[/latex] to get the reciprocal [latex]\Large\frac{5}{two}[/latex].

Division past Zilch

You lot know what it ways to divide by [latex]2[/latex] or split up by [latex]10[/latex], but what does it mean to divide a quantity past [latex]0[/latex]? Is this fifty-fifty possible? Tin can yous separate [latex]0[/latex] past a number? Consider the fraction

[latex]\Large\frac{0}{8}[/latex]

We can read information technology as, "zippo divided by eight." Since multiplication is the inverse of division, we could rewrite this equally a multiplication problem.

[latex]\text{?}\cdot{viii}=0[/latex].

Nosotros can infer that the unknown must be [latex]0[/latex] since that is the but number that will give a outcome of [latex]0[/latex] when it is multiplied past [latex]8[/latex].

At present permit's consider the reciprocal of [latex]\Large\frac{0}{eight}[/latex] which would be [latex]\Large\frac{viii}{0}[/latex]. If nosotros rewrite this as a multiplication problem, we will take

[latex]\text{?}\cdot{0}=eight[/latex].

This doesn't make whatever sense. In that location are no numbers that y'all can multiply past goose egg to become a result of 8. The reciprocal of [latex]\Large\frac{8}{0}[/latex] is undefined, and in fact, all partition by aught is undefined.

Circumspection! Segmentation past zippo is undefined and so is the reciprocal of whatever fraction that has a naught in the numerator. For any real number a, [latex]\Large\frac{a}{0}[/latex] is undefined. Additionally, the reciprocal of [latex]\Large\frac{0}{a}[/latex] volition always exist undefined.

Divide a Fraction by a Whole Number

When you lot divide past a whole number, you are multiplying by the reciprocal. In the painting example where yous demand [latex]three[/latex] quarts of paint for a glaze and take [latex]6[/latex] quarts of paint, you can notice the total number of coats that tin can be painted by dividing [latex]6[/latex] by [latex]iii[/latex], [latex]6\div3=2[/latex]. You can likewise multiply [latex]6[/latex] past the reciprocal of [latex]iii[/latex], which is [latex]\Large\frac{1}{3}[/latex], and so the multiplication problem becomes

[latex]\Large\frac{six}{1}\cdot\Large\frac{1}{3}=\Large\frac{6}{3}=\normalsize2[/latex]

Dividing is Multiplying past the Reciprocal

For all division, you lot can turn the operation into multiplication by using the reciprocal. Dividing is the same as multiplying by the reciprocal.

The same idea will work when the divisor (the affair being divided) is a fraction. If y'all have [latex]\Large\frac{three}{four}[/latex] of a candy bar and need to divide it amid [latex]v[/latex] people, each person gets [latex]\Large\frac{1}{5}[/latex] of the available candy:

[latex]\Big\frac{1}{5}\normalsize\text{ of }\Large\frac{3}{four}=\Large\frac{one}{5}\cdot\Large\frac{3}{iv}=\Large\frac{3}{20}[/latex]

Each person gets [latex]\Large\frac{3}{20}[/latex] of a whole candy bar.

If you accept a recipe that needs to be divided in half, you can carve up each ingredient past [latex]ii[/latex], or you can multiply each ingredient past [latex]\Large\frac{1}{two}[/latex] to notice the new amount.

For example, dividing by [latex]6[/latex] is the same as multiplying past the reciprocal of [latex]6[/latex], which is [latex]\Large\frac{ane}{6}[/latex]. Look at the diagram of two pizzas below.  How can you carve up what is left (the crimson shaded region) among [latex]6[/latex] people fairly?

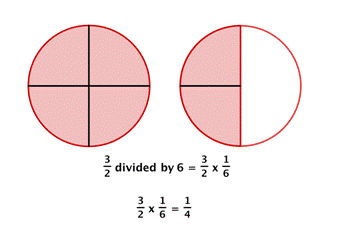
Each person gets one piece, then each person gets [latex]\Large\frac{1}{4}[/latex] of a pizza.

Dividing a fraction by a whole number is the same as multiplying past the reciprocal, so you tin ever use multiplication of fractions to solve sectionalisation problems.

Example

Find [latex]\Large\frac{two}{iii}\div \normalsize 4[/latex]

Instance

Split up. [latex] 9\div\Large\frac{ane}{ii}[/latex]

Divide a Fraction by a Fraction

Sometimes you demand to solve a problem that requires dividing past a fraction. Suppose you accept a pizza that is already cut into [latex]4[/latex] slices. How many [latex]\Big\frac{1}{ii}[/latex] slices are there?

There are [latex]8[/latex] slices. Yous can see that dividing [latex]4[/latex] by [latex]\Large\frac{i}{2}[/latex] gives the same issue as multiplying [latex]4[/latex] past [latex]2[/latex].

What would happen if you needed to split each piece into thirds?

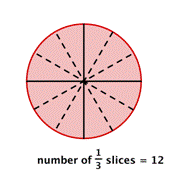
You would accept [latex]12[/latex] slices, which is the aforementioned as multiplying [latex]4[/latex] past [latex]iii[/latex].

Dividing with Fractions

1. Find the reciprocal of the number that follows the sectionalization symbol.
2. Multiply the first number (the one before the partition symbol) by the reciprocal of the second number (the 1 subsequently the division symbol).

Any piece of cake way to remember how to divide fractions is the phrase "keep, change, flip." This means to Go along the first number, CHANGE the division sign to multiplication, and then FLIP (use the reciprocal) of the second number.

Case

Divide [latex]\Large\frac{2}{three}\div\Large\frac{one}{half-dozen}[/latex]

Example

Divide [latex]\Large\frac{3}{5}\div\Large\frac{2}{3}[/latex]

When solving a segmentation problem by multiplying by the reciprocal, retrieve to write all whole numbers and mixed numbers as improper fractions. The final reply should be simplified and written as a mixed number.

In the following video yous will come across an example of how to divide an integer by a fraction, too equally an example of how to split up a fraction by another fraction.

ivesbrines.blogspot.com

Source: https://courses.lumenlearning.com/waymakercollegealgebracorequisite/chapter/review-operations-on-fractions/

Share this post